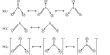
In 1884 English physicist John Henry Poynting (1852-1914) published his theorem, which is an expression of the law of conservation of energy in electrodynamics. We shall obtain Poynting’s theorem from Maxwell’s equations by taking the dot product of E with Ampere’s Law and the dot product of H with Faraday’s Law to obtain
E * (Δ * H) = E (J + ϐD/ϐt) …. … …. (1)
H * (Δ * E) = H * [-(ϐB/ϐt)] …. …. ….(2)
Subtracting Eq.1 from Eq.2 gives;
E * (Δ * H) – H * (Δ * E) = E * J + [ E * ϐD/ϐt + H * ϐB/ϐt]
Then using the product rule Δ • (e x h) = h • (Δ x e) — e • (Δ x h) we obtain
– Δ • (E x H) = E . J + [ E * ϐD/ϐt + H * ϐB/ϐt]
Taking the volume integral of both sides, and then using Gauss’ theorem on the left hand side we get Poynting’s Theorem:
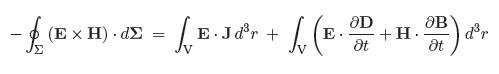
where d∑ is the surface element, and surface ∑ bounds volume V.
Thus we define the Poynting Vector
S ≡ E * H
which gives the energy flux (W m-2) carried by the electromagnetic field, and points in the direction of energy flow.