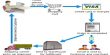
In both circular and elliptical polarisation the electric and magnetic field vectors rotate with angular frequency w. In circular polarisation E0,y = E0,x ≡ E0 and (ϐy – ϐx) = ± π/2, so that the locus of the tip of the E vector undergoes circular motion with “radius” E0 in the Ex –Ey plane and angular frequency w, as shown in the Fig (a). This means that the EM wave is circularly polarised. There are two possibilities depending on the sign of (ϐy — ϐx), usually referred to in optics textbooks as right or left polarisation, or to use particle physics nomenclature negative or positive helicity, respectively. Note that we are free to define ϐx = 0.
When discussing Faraday rotation, it will be useful to use new complex basis vectors for circularly polarised waves propagating in the + Z direction,
eR = (x — i y), eL = (x + iy)
Note that these basis vectors are not actually unit vectors as their magnitudes are both √2 rather than 1 (I have deliberately omitted the hat symbol), but we shall find them useful in their unnormalised. Then for right circular polarisation,
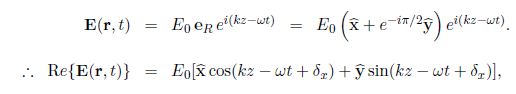
and for left circular polarisation,
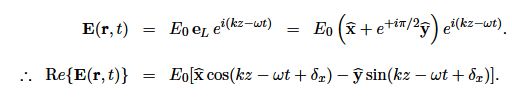
In Fig (a) we are located at some fixed z, and view the wave coming towards us. If you bend your fingers and point your thumbs in the direction of the source of the wave (i.e. thumbs point in the — Z direction), and if the fingers of your right hand curl in the direction of rotation of the E vector then the polarisation is “right-handed”. Fig shows a wave which is right-circularly polarised. Note that this is the usual convention used in optics.
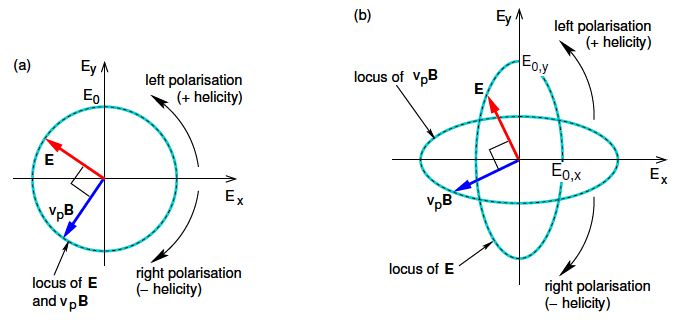
Figure: Loci of the tips of the E and vp B vectors in the Ex—Ey plane as observed at fixed z for (a) circular polarisation and (b) elliptical polarisation. (The wave is propagating in the +Z direction.)