A magnetic dipole of moment M = mz is located at the origin. A thin circular conducting ring of radius a vibrates such that the position of its centre is r = [z0 + b cos (ωt)]z with b << a < 20. The plane of the ring remains parallel to the x—y plane during the vibration. Find the emf around the ring in the φ direction.
So, The magnetic field of the dipole is
B (r) = μ0 / 4π [ {3r (m.r) – r2m} / r5]
Since b << a < z0 we can approximate the magnetic field anywhere on the ring as it vibrates by
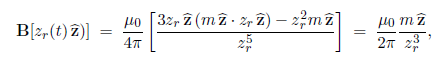
Where, zr(t) = [z0 + b cos (ωt)]z, is the height of the ring.
The magnetic flux through the loop is:
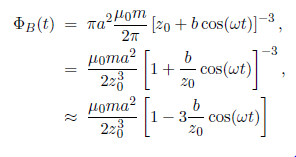
Since a << z0. Hence,
Ɛ = – (dφB / dt)
So, Ɛ ≈ – [ 3μ0ma2bω / 2z04] sin (ωt)