The amplitude coefficients for the case of internal reflection r┴ , t┴, r‖ and T‖ are plotted in Fig (a) for flint glass to air. There is a critical angle of incidence θc such that if θi > θc Snell’s law cannot be satisfied as sin θt would need to exceed 1. For θi > θc there will be no trsmcmicksion, t = 0, but there will be total internal reflection, ӏrl = 1. From Snell’s law with θt = 90° the critical angle is
θc = sin-1 (nt/ni)
For internal reflection nt < ni, and so √ [(nt / ni)2 – sin2 θi] is either real if < Ot or imaginary if θi > θc. Hence, for θi > θc the amplitude reflection coefficients are real, and so the phase shift is ϕ = 0° if r > 0 and ϕ = 180° if r < 0, as was the case for external reflection. However, for θi > θc the amplitude reflection coefficients are complex, and what is plotted in Fig (b) for θi > θc is actually ӏr┴ӏ and ӏT‖ӏ.
Adopting the convention used in optics texts for the sign of ϕ the amplitude reflection coefficient is defined r = ӏ r ӏ e-iϕ The phase shift ϕ may then be derived by noting that for θi > θc equation may be written in the form;
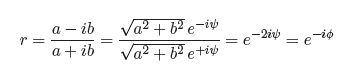
and so the phase shift is: ϕ = 2 tan-1 (b/a)
where b = √ [sin2 θi — (nt/ni)2] , and for perpendicular polarisation a = cos θi and for parallel polarisation a = (nt/ni)2 cos θi. The resulting phase shifts are plotted in Fig (b).
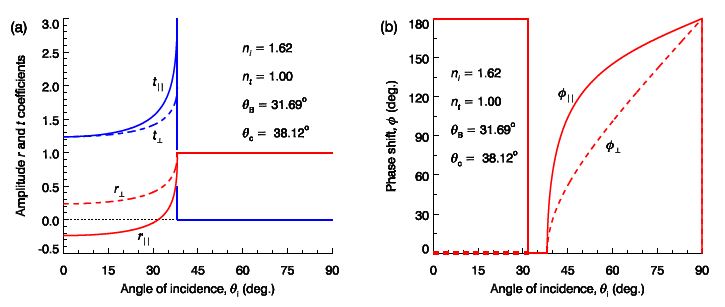
Figure: (a) Amplitude reflection and transmission coefficients, and (b) phase shift, for internal reflection within flint glass. (For θi > θc in part (a) r┴ and r‖ is plotted.)