One of the most obvious uses of matrices is to organize the data of several simultaneous equations in a compact form so it can be manipulated and easily solved. This is most commonly used in Analytical Chemistry. A set of linear simultaneous equations consisting of numerical values for the coefficients A and the values b can be solved for the unknown variables x when it is written in matrix form A x = b. As we need as many simultaneous equations as there are unknown variables we will have a square matrix for A. If we multiply by the inverse of A on both sides it gives A-1 Ax = A-1 b, or Ix = A-1 b where I is the identity matrix and so x = A-1 b. So the problem is reduced to finding the inverse matrix. To find the inverse we have to do several things, firstly find the determinant of A, ׀A׀, and secondly, the matrix of cofactors of A, C, and then the transpose of C (CT = adj A the adjunct of A). Here is a simple remilnder of these steps for the set of simultaneous equations below we have the A matrix,
5 x1 + 2 x2 + 3 x3 = 4
4 x1 + l x2 + 6 x3 = 3
8 x1 + 0 x2 + 7 x3 = – 2
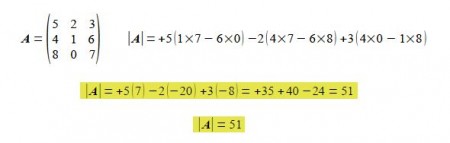


Substituting in for the determinant of A, the transpose of cofactors (CT the adjunct of A), and the values for b
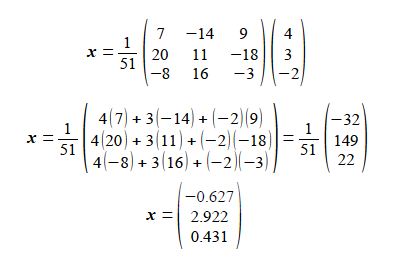
Solving small numerical matrices by hand may be fine and it is something you need to do for exam questions! But for large matrices I will show you later a simple spreadsheet approach.
A second use of matrices in Chemistry is the efficient handling of the symmetry operations that apply to molecules. The shape of molecules is one of their most important properties and the shape is defined by the symmetry operations that they can undergo. A molecule has a particular shape or symmetry which may be transformed in three-dimensional space by rotations around its symmetry axes; reflections in its mirror planes; rotation-reflection (or improper rotation); inversions through a centre of symmetry; and the identity operation.
A third area in Chemistry where matrices are used is the eigenvalues and eigenvectors of the determinant of square a matrix to find the allowed solutions to the quantum mechanics of the structures and reaction pathways of a molecule.