Energy in the form of heat can be transported when a driving force in the form of a temperature difference is applied. The flux of heat is proportional to the applied driving force and the proportionality constant is called the thermal conductivity k. We are talking about molecular Transport of Energy, and a situation with transport of heat through a one layer window is sketched in below Figure.
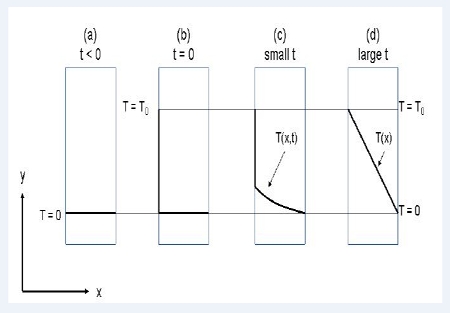
(a) The temperature on both sides of the window is zero. (b) At t= 0 the temperature on the left side of the window is increased to T0. (c) Energy/heat starts to flow through the window. At small values of t, the temperature in the window is thus a function of both time and distance x in the window. (d) At large values of t, steady state is established and a linear temperature profile in the window is reached. Thus at steady state the temperature is only a function of the distance x in the window.
Initially the temperature on both sides of the window is zero (or room temperature) which means that no heat flow through the window. Suddenly at t = 0 the temperature on the left side of the window is increased to T0. Because of the temperature difference between the two sides of the window heat starts to flow through the window from the warm side to the cold side. The temperature on the right side is kept at zero. Before steady state is reached the temperature in the window is a function of both distance x and time 1. Dependent of how good or bad an isolator the window is, a linear steady state temperature profile is reached after a period of time.
At steady state the flux of heat/energy through the window is given by the flux equation from Table, which is called Fourier ‘s law of heat conduction:
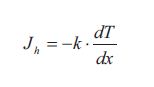
The flux Jh is the flux of heat/energy in the direction x through the window. The gradient dT/dx is the temperature gradient which is the driving force. The term k is as mentioned earlier the thermal conductivity of the window. The value of the thermal conductivity together with other factors determines how fast the linear steady state temperature profile develops. These other factors are the density p and the heat capacity Cp of the window. The thermal conductivity, the density and the heat capacity can together be expressed at the thermal diffusivity a:
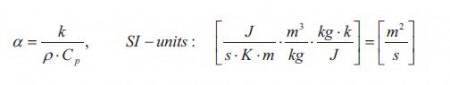
It is seen form equation that the thermal diffusivity has the same units as the ordinary diffusivity D. Thus the thermal diffusivity can be thought of a diffusion coefficient for energy/heat. The thermal diffusivity of the window thus determines how fast the steady state temperature profile is established:
The larger the thermal diffusivity a (of the window) is, the faster the linear steady state temperature profile is reached. If a is small the flux of heat/energy is small and the time before steady state is reached is large.
The thermal conductivity of gasses is of course dependent on the pressure but also on the temperature. Thermal conductivities of liquids and solids are also temperature dependent but almost pressure independent in the pressure range where they are almost incompressible. Further discussion about pressure and temperature dependence will not be given in this text.











