The Rydberg equation very accurately summarizes the UV-visible electronic spectroscopy that is observed for the hydrogen atom. It gives the wavenumber f, (pronounced “nu bar”) of the light emitted or absorbed by a Hydrogen-atom in terms of jumps of the single electron between two quantized energy levels.
V = RH [ 1/n12 – 1/n22]
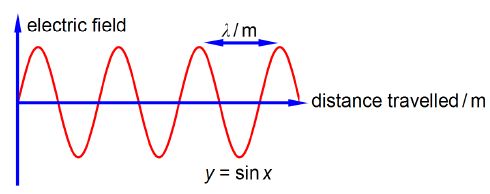
Wavenumber (units of cm-1 pronounced as ‘centimetres to the minus one” or “reciprocal centimetres”) is for the wave nature of light the number of complete light waves per centimetre as in below Figure.
The quantized energy levels are called atomic orbitals (AOs) and are characterized by the two principal quantum numbers n1 for the initial AO and n2 for the final AO involved in the jump. RH is the Rydberg constant. Rearrange the equation to obtain n2 as the subject of the equation.
Rearranging to obtain n2 as the subject of the equation is a bit more difficult than it may appear at first sight.
(1) Expand out the bracket;
(2) bring the term involving n2 to the left hand side by adding RH /n22 to both sides and then cancelling out where possible;
V = [RH / n12 – RH / n22] or, [V + RH / n22] = RH / n12
(3) nu-bar is moved to the right hand side by subtracting nu-bar from both sides and then cancelling out;
RH / n22 = [RH / n12] – V
(4) bring the right hand side to a common denominator of n12 ;
(5) divide left and right by RH and then cancel out on the left hand side of the equals sign but not on the right hand side because of the minus sign, here the numerator consists of two terms;
(6) take reciprocals on both sides;
(7) take square root of both sides.
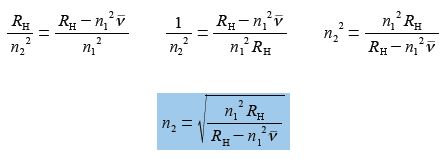
Which is the correct equation with n2 as the subject, however, you may have realized that n1 in the numerator can be square rooted and taken outside the bracket to give an equally correct version. On the other hand n1 in the denominator cannot be square rooted because of the minus sign, as the denominator is made up of two terms which must both be treated equally.
n2 = n1 √[RH / n12V]