Van’t Hoff’s Laws of Osmotic Pressure
Quantitative relations between the concentration of the solution and the osmotic pressure were first derived by van’t Hoff in 1886. These are known as van’t Hoff’s laws of osmotic pressure. The van’t Hoff theory describes that substances in dilute solution obey the ideal gas laws.
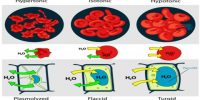
The van’t Hoff theory describes that substances in dilute solution observe the ideal gas laws, resulting in the osmotic pressure. Osmotic pressure also reflects how eagerly water can enter the solution via osmosis, as transversely a cell membrane. Osmotic pressure arises when an uncontaminated solvent is alienated by a semi-permeable membrane from a solution containing a solute that is impermeable through the semipermeable membrane. For a dilute solution, osmotic pressure obeys a structure of the ideal gas law and can be intended provided you know the absorption of the solution and the temperature.
First law: The osmotic pressure (π) of a solution is directly proportional to the molar concentration of the solute at a constant temperature. Mathematically,
π ∞ c (T = constant) … … … (1)
or, π ∞ 1/V (since c = 1/V)
and, πV = constant … …. (2)
Where c is the concentration of the solution in mol L-1 and V is the volume containing one mole of the solute. Equation (2) is similar to Boyle’s law for gas pressure. He found that the solute particles in dilute solutions possess kinetic energy and move in random directions in the solutions. Thus they have related activities as that of gas molecules.
Second law: The osmotic pressure of a solution of given concentration varies directly as the temperature in Kelvin (K). Expressed mathematically,
π ∞ T (e = constant) … … … (3)
or, π = KT … … … (4)
Equation (4) is similar to Charles’ law for gas pressure. The osmotic pressure of a gas is directly proportional to absolute temperature. On collision alongside semi-permeable membrane, the solute molecules exert osmotic pressure equivalent to the pressure which the solute molecules would exert if it were gas molecule at the similar temperature and occupying the similar volume as that of solution.
Third law: Equimolecular quantities of different solutes dissolved in such volumes of the solvent as to give the same volume of the solution have the same osmotic pressure at the same temperature. Thus the gas laws are regularly relevant to dilute solutions.
Laws of variation are used to combine equations (1) and (3) to give equation (5).
π = K’cT
or, πV = nK’T … … … (5)
Where n is the number of moles of the solute in V L of the solution and K’ is the proportionality constant, van’t Hoff also found that K’ has the same value as the universal gas constant, R, so that equation (5) may be written as-
πV = nRT
or π = (n/V)RT = cRT
This is the general form of osmotic pressure equation. Thus the osmotic pressure equation is exactly analogous to the ideal gas equation including the numerical value of the constant R.
van’t Hoff’s assumption of the osmotic pressure, for which he received the first Noble prize in chemistry, was not normally accepted in the years that followed and was replaced by an analysis in terms of chemical potentials.