The Third Law of Thermodynamics
The second law of thermodynamics leads to the definition of entropy and calculation of differences of entropy. We have seen that entropy is a measure of chaos in a system. When a system goes from an ordered state to a disordered state the entropy is increased. The converse is also true. But the second law does not allow calculation of absolute value of the entropy of a system. The third law of thermodynamics developed by Ludwig Boltzmann offers a method of calculating the absolute value of entropy.
The law can be stated in different forms;
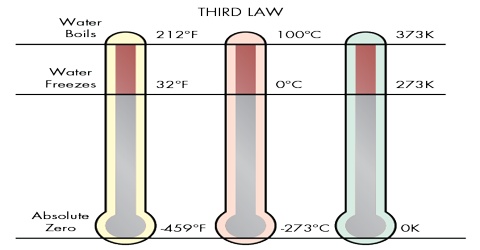
(1) “It is impossible to attain the absolute zero of temperature”. (W. Nernst, 1912)
(2) “The entropy of a solid or liquid chemically homogeneous substance has the value of zero at the absolute zero of temperature”. (M. Planck. 1912)
An alternative definition of the third law of thermodynamics was given by Gilbert N. Lewis and Merle Randall in 1923-
“Every substances has a finite positive entropy, but at the absolute zero of temperature the entropy may become zero and does so become in the case of a perfectly crystalline substance.”

The third law of thermodynamics gives us an opportunity to calculate the absolute entropy of a system at any specified temperature. Consider that at solid to transform at constant pressure from 00 C to some temperature, T, below its melting point:
Solid (0°K) → Solid (T)
The value of the entropy of an element at any temperature can be obtained from careful measurements of the heat capacity CP of the element from the desired temperature down to absolute zero. However, since the measurements of heat capacity at very low temperature, e.g. about 15 K or below, do not yield accurate results, use is made of Debye’s equation for specific heat of solids at low temperatures; that is,
CV = aT3
where ‘a’ is a constant. At such low temperatures CP and CV are not different. Since the constant ‘a’ may be determined from experiments at the lowest temperature at which accurate measurements are possible Debye’s equation is used to evaluate CP up to the lowest temperature of measurements, say 15 K. The value of CV = CP = aT3, is substituted in equation to obtain the entropy upto 15 K. When CP is not constant but is known as a function of temperature the entropy of a substance from 15 K to temperature T is evaluated by plotting either CP / T against T or CP against log T. The area under the curve is the value of the integral from 15 K to the temperature T. If there is a phase change in the interval of temperature used the entropy changes for the phase change is calculated in the usual manner. The sum of all these values gives the entropy of the substance at temperature T.
It should be mentioned that unlike the other laws of thermodynamics the third law is not based on experiments and is applicable only to special class of compounds, namely pure, crystalline solids. The law has, however, been extremely useful in obtaining absolute values of entropy. The agreement in many cases of such entropy values with those calculated from a totally different concept, namely molecular spectroscopy, lends support to the validity of the law.