Thermodynamic Derivation of Osmotic Pressure Laws
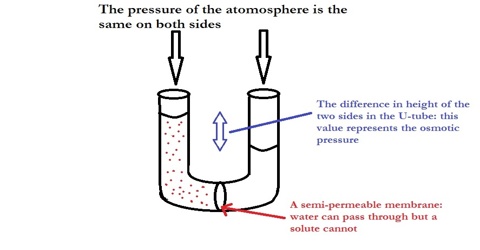
The laws of osmotic pressure can be deduced in a number of ways by thermodynamic principles. Only one is given which makes use of the Raoult’s law of lowering of vapour pressure. Let us take the pure solvent and the solution in two chambers separated by a semi-permeable membrane and let the equilibrium be established at constant temperature T (Figure).
Let p° and p be the vapour pressures of the solvent and solution respectively. A cyclic process comprising the following isothermal reversible steps may be imagined to be carried out.
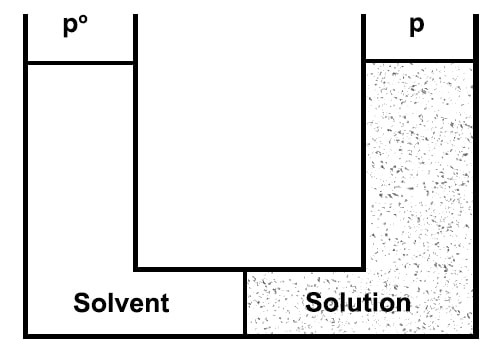
Figure: Semi-permeable membrane separating solvent from solution
(1) dx mole of the liquid solvent is converted to the vapour phase from the solvent chamber.
Work done w1 = dx RT … … … (1)
(2) dx mole of the vapour is transferred to the solution side and expanded pressure p° to p.
Work done w2 = – dx RT ln (p°/ p) … … … (2)
(3) dx mole of the vapour is condensed at pressure p on the solution side.
Work done w3 = – dx RT … … … (3)
(4) dx mole of the solvent is now transferred through the semi-permeable membrane from the solution side to the solvent side by applying a pressure infinitesimally greater than the osmotic pressure π.
Work done, w4 = – dx πV’ … … … (4)
where V’ is the volume of 1.00 mole of the solvent
The total work done by this isothermal and reversible process is obtained by adding all the work terms in the four steps. Since a cyclic process has been completed isothermally and reversibly the network is zero. Therefore,
dx = RT+ dxRT ln (p°/ p) – dx RT – dx πV’ = 0
or, πV’ = RT ln (p°/ p) = RT ln [1 + (p°- p)/p]
= RT (p°- p)/p = RT n/N
or, πV’ x N/n = RT (for dilute solution (p°- p)/p = (p°- p)/p0]
If n moles of the bolt are associated with N moles of solvent then one mole of the solvent will contain n/N moles of solute. Therefore, V’ x N/n = V, which represents the volume of the solution containing one mole of the solute.
Or, πV = RT