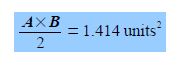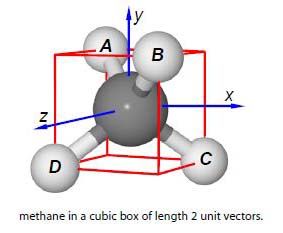
Methane is tetrahedral, that is it fits inside a cube with the carbon atom at the intersection of any two diagonals, which is at the origin (0, 0, 0), above Figure. Two hydrogen atoms sit on the top face at the ends of a “horizontal” diagonal and the other two hydrogen atoms are on the bottom face at the ends of the other “horizontal” diagonal. Firstly, if the cube has sides of length 2 unit vectors calculate the bond vectors from the C-atom to each H-atom A, B, C and D. Secondly, choose any two bonds and use the vector product (scalar product) to calculate the angle between them. Thirdly, choose any two bonds and use the vector product (cross product) to calculate the area of the triangle formed by these two bonds.
Solution
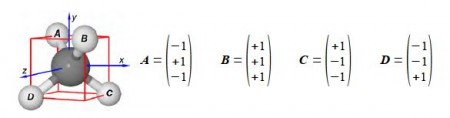
From the C-atom (at the origin) to the H-atoms the four bond vectors are given in above Figure. Secondly, if A and B are two vectors with components Ax, Ay, Az, and Be Be Br with an angle 0 between them, then the scalar product (or dot product) may be written in either of two ways.
A • B = Ax Bx + Ay By + Az Bz = ׀A׀ ׀B׀ Cosθ (The scaler product or dot product)
The scalar product as its name implies is a scaler quantity and is used most often in Chemistry to find the angle between two vectors and also for the potential energy of a magnetic dipole in a magnetic field (e.g. electron spin ESR and nuclear spin NMR). Choosing A and B as the two bond vectors (it doesn’t matter which pair you choose) we have for the left hand side of the scalar product.
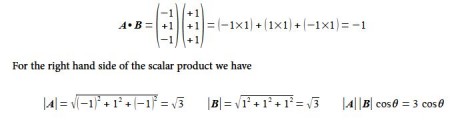
equaling the two sides of the scaler product gives us the angle between the two C-H bonds in methane which is the tetrahedral angle.
-1 = 3 cosθ, θ = 109.5°
Thirdly, we are asked for the area of the triangle formed by the C-atom and any two H-atoms, this is obtained by using the vector product or the cross product. An area can be represented by a vector at right angles to the surface of the parallelogram formed from the two vectors A and B as in below Figure.
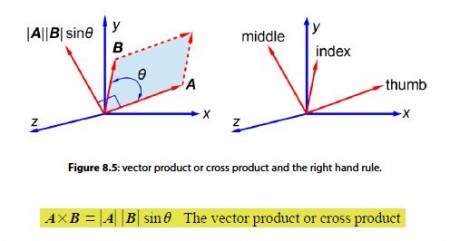
The direction of the vector AxB is found from the right hand rule. Arrange your thumb, index and middle fingers of your right hand at right angles to one another, align the thumb with the first vector A, then align the index finger with the second vector B, then the middle finger points in the direction of the third vector, the cross product IAI IBIsinθ, i.e. you count 1, 2, 3 from your thumb for the three vectors A, B, and their vector product.
A x B = √3 x √3 x sin 109.5° = 2.828 units2
This the area of the parallelogram but we only want half of this for the triangle formed by vectors A and B.