The Principle of Equipartition of Energy
The principle of equipartition of energy states that the total energy of a molecule is divided equally among the different degrees of freedom. A degree of freedom is defined as an independent mode in which a body may be displaced. We know that, the translational motion of a body may be resolved into three components along three mutually perpendicular directions. Thus, a body may have three translational degrees of freedom, one for displacement or motion along each direction. We also know that the velocities of molecules along the three directions may be taken as equal so that one can write, for a molecule of mass m, the following for the K.E. of the molecule;
½ mu2 = ½ mv2 = ½ mw2
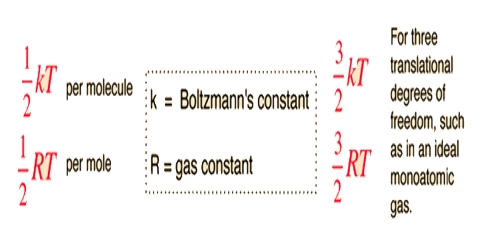
Again, the K.E. of an Avogadro number of molecules = 3/2 RT
Or the for one molecule K.E. = 3/2 T.(R/N), i.e., =-3/2 kT; where k is known as the Boltzmann Constant. According to the principle of equipartition of energy the contribution from each degree of freedom to the total K.E. of one molecule is 1/2 kT or that of one mole is ½ RT.
Consider now rotational motion of molecules. It can be easily visualized that a polyatomic molecule may have three rotational degrees of freedom for rotation around three mutually perpendicular axes. For a diatomic molecule or a linear polyatomic molecule there are only two rotational degrees of freedom as rotation around the axis of a molecule does not contribute to the total energy of the molecule. Each of the degrees of freedom for rotational motion will contribure ½ kT molecule-1 or ½ RT mol-1 to the total energy of the molecules. Monatomic molecules do not have rotational contribution to energy.
Molecules containing more than one atom have vibrational motion along the bonds as well as bending vibrations. Energy due to each vibrational motion has two components- one kinetic and one potential. Each component contributes ½ kT molecule-1 or ½ RT mol-1 to the energy of the molecules. Hence each vibrational degree of freedom contributes;
2 x ½ kT molecule-1 or, 2 x ½ RT mole-1
It may be shown that a molecule containing N atoms has a total of 3N degrees of freedom. For a diatomic or a linear polyatomic molecule there are three translational degrees of freedom and two rotational degrees of freedom.
Hence the number of vibrational degrees of freedom is (3N – 5). For a non linear polyatomic molecule there are three, rotational degrees of freedom and hence (3N – 6) vibrational degrees of freedom.
These results are of great importance as they allow the calculation of the total energy and hence the molar heat capacity of the molecules.
It should be mentioned that complicating factors must be taken into account for obtaining correct value of molar heat capacities from the energy values obtained with the help of the principle of equipartition of energy.