New batteries for car, laptops, tablet computers and mobiles are developed by Chemists. These batteries are now made from polymer electrolytes as these can offer significant performance improvements.
One tool that is often used to characterize the behavior of these polymer electrolytes is the technique of impedance spectroscopy, where the electrical impedance Z of a sample is measured as a function of an applied alternating current of angular frequency ω. The impedance Z is the opposition to the flow of an alternating current and is measured in ohms. Angular frequency ω = 2π/T where T is the period of rotation in seconds, so ω is in radians/second and is equals 2πv where v is the ordinary frequency in hertz or s-1. It is found experimentally that some materials exhibit an impedance response that is given by the following equation
Z(ω)=Rο/(1+iωT)
Where R0 is the direct current (DC) resistance of the polymer electrolyte and is a constant and τ (tau) is the time. It is found that impedance is a complex variable,
Z(ω)=x(ω)+iy(ω)
Firstly, find the expressions for the real and the imaginary parts of the impedance equation i.e. find expressions for both x(ω) and y(ω). Secondly, eliminate τπ from these equations and graph Z(ω) in the complex plane as a function of w and show it is a circle. Find the (x, y) coordinates of its centre and the radius of the circle. For a good polymer electrolyte for a new battery, we will needs a high ionic conductivity i.e. a low DC resistance, R0. As a hint the equation for a circle with its centre at (a, b) and radius r is,
(x- a)2 + (y – b)2 = r2
Solution
This has a similar solution to the last question but with a twist in the plot! First evaluate the real and imaginary parts by multiplying top and bottom by the complex conjugate.
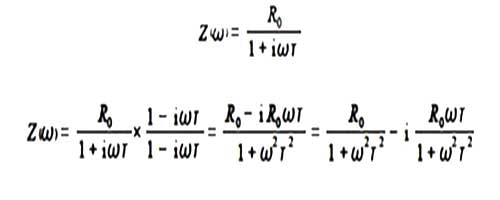
In impedance spectroscopy this is usually written as below which gives us the twist that y(ω) is a function of x (ω),
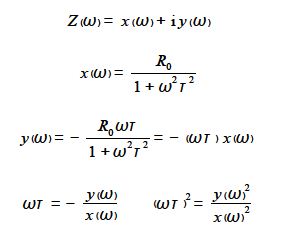
Thus on substituting for (πτ)2 in the equation for the real part of the impedance, x(ω), and for clarity dropping the reminder that x and y are both functions of the angular frequency ω we have,

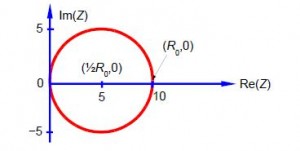
As suggested in the question, this is the equation for a circle with centre at (1/2R0, 0) and radius ½ R0, with the circle lying in the x-y plane (the Re(Z)-Im(Z) plane) as in below Figure which is drawn for R0 = 10 ohms.