Balancing by inspection:
Consider the example:
![]()
We notice that there are 2 nitrogens on both the left and right sides, so nitrogen is already balanced. There are 3 oxygens on the left but only 2 on the right, so oxygen is not balanced. Similarly, there are 4 hydrogens on the left and only 2 on the right, so hydrogen is not balanced. The balancing of oxygen and hydrogen can be handled together by making the coefficient of H2O equal to 2.
Then, the balanced equation reads:
![]()
Now there are equal quantities of all elements on both sides of the reaction, and mass conservation is satisfied. Balancing by inspection in this way is quick and useful when you can see the solution easily.
Algebraic method:
Consider the reaction:
![]()
This equation could be balanced by inspection. However, we will use it to illustrate another approach – the algebraic approach. To balance a reaction algebraically, we start by putting unknown coefficients in front of each molecular species in the equation:
![]()
Then we write down the balance conditions for each element in terms of the unknowns. In this case, there are are four unknowns, x, y, z and w. From carbon balance, we have the condition:
![]()
The hydrogen balance condition is:
![]()
and the oxygen balance condition gives:
![]()
This constitutes a set of only three equations for the four unknowns. The fourth condition comes from recognizing that chemical equations specify relative amounts of reactants and products. Thus, one of the coefficients is arbitrary, and all the others can be expressed relative to it. Thus, we may take one of the coefficients to be 1, arbitrarily, which then leaves only three unknowns and three conditions to determine them. The choice of which coefficient to set to 1 is completely arbitrary and may be taken to be the one that is most convenient for solving the problem. In this case, the choice $x=1$ allows us to arrive at a solution almost immediately, for then it follows that z=4 and w=5. From the oxygen balance condition, y can be determined to be 2y=8+5=13 so y=13/2. Thus, the balanced equation could be written as:
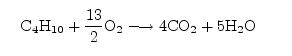
This is a perfectly fine way of writing the equation, however, customarily, it is preferable to express all the coefficients as integers, in accordance with the law of combining volumes and Avogadro’s hypothesis. Thus, we can multiply through the equation by 2 on both sides (it can be treated as an algebraic equation in this way) and obtain the final result:
![]()
As a second example, consider the reaction:
![]()
Again, we put unknown coefficients in front of each molecular species:
![]()
Writing down the balance conditions on each element gives:
Sodium balance: x = 2u
Chlorine balance: x = v
Sulfur balance: y = u
Oxygen balance: 2y + z + 2w = 4u
Hydrogen balance: 2z = v
Setting u=1 arbitrarily, gives the immediate solution: x =2, v=2, y=1, z=1
and 2+1+2w = 4 or w=1/2. In order to clear the fraction, we multiply all the coefficients by 2 and write down the balanced equation:
![]()