Measurement of Transference Number: Moving boundary method:
Transference Number may be measured by different methods, e.g., Hittorf’s method, moving boundary method and from the electromotive force of concentration cells.
Here briefly focus on Moving boundary method –
This method is based on the direct observation of the migration of ions under the influence of an applied electric field. Let us consider Hydrochloric acid and the transport numbers of H+ and CI ions present in HCI have to be determined. The hydrochloric acid is called the principal or experimental electrolyte. Another electrolyte containing a common ion (Cl-) called the indicator electrolyte is selected. The speed of the cation of the indicator electrolyte is selected. The speed of the cation of the indicator electrolyte should be less than that of the cation of the experimental electrolyte. For example – CdCl2 can be selected as the indicator electrolyte as the speed of Cd++ ion is less than that of H+ ions. A concentrated solution of CdCl2 is used so that HCI solution can float on it. The moving boundary method utilizes this principle. The arrangement is shown in Figure.
The solution of an electrolyte MA, which is to he studied, is placed between the solutions of two other salts MA’ and MꞌA such that MꞌA has the anion A common with MA and MA’ and MA have the common cation M. The salts are to be so chosen that the densities increase downwards. Also, the speed of the ion Mꞌ should be less than that of M while the speed of A’ should be less than that of A ion.
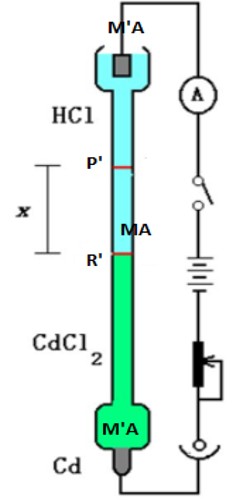
Figure: Moving boundary method
This is essential to maintain sharp boundaries between the three solutions of electrolytes. The initial sharp boundary between the solutions of MꞌA and MA is shown by the horizontal line P whereas the initial sharp boundary between MA’ and MA is shown by R. In passing current from the source B ionic migration starts and the boundary P moves downwards, say to P’, while the boundary R moves to R’. The distance traveled by the two boundaries in time t are PP’ and RRꞌ, which are directly proportional to the cationic and anionic velocities respectively. Therefore,
t+ = u+ / ( u– + u+) = PP’ / (PP’ + RRꞌ)
t– = u– / ( u+ + u–) = RR’ / (RR’ + PPꞌ) … …. … (14.23)
The transport numbers are thus measured. It should be noted that electrolytes MA, MA’ and M’A should he have carefully chosen to get good results. In practice, it is necessary to form one boundary and observe the rote of its movement to measure the transference number of one ion, that of the other ion may then be calculated as t+ + t– = 1.
Under this condition the transference number is calculated as follows: Suppose that the boundary of the moving cation is swept through a distance ‘l’ in a tube of cross-section ‘a’, so that the volume swept out by the passage of Q coulombs of electricity is (l x a). If 1F of electricity flows through the solution t, the equivalent mass of cation must pass through any given point. Let c, be the concentration of the solution is equivalent mass L-1; then the volume of solution contenting ‘l’ equivalent man of electrolyte is 1000/c. Hence during the passage of 1 F of electricity, the canon boundary will sweep through a volume 1000/c t+. For the passage of Q coulombs, therefore, the same boundary will sweep out a volume of –
(1000 x t+ x Q) / (c x F)
Hence, l x a = (1000 x t+ x Q) / (c x F)
or, t+ = (l x a x c F) / 1000Q.