Measurement of Surface Tension in Drop formation method:
Figure shows a drop of liquid forming at the end of a capillary tube of radius r.
As the liquid slowly extends from the tip of the tube, the excess liquid is held to the tip of the tube by the surface tension forces. As the volume of the extended mass of the liquid increases, the drop finally breaks off when the surface force can no longer support the mass of the drop. At the instant the drop breaks, the gravitational force on a drop of mass m equals the surface tension force.
mg = 2πr γ … … … (1)
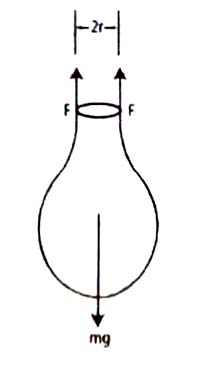
A drop forming at the tip of capillary tube of radius r
In Practice the mass of a number of drops are taken from which the average value for one drop is calculated.
Example: A drop pipette of radius 0.40 cm was used to slowly drop a liquid at 25°C in the form c4 small drops which were collected in a weighing bottle. If the mass of 20 drops of the liquid was 1.052 R. calculate the surface tension of the liquid at this temperature. (g = 980 cms sec-2)
Solution: Substituting the values of the different quantities in equation (1) we obtain,
1.052/20 x 980 = (2 x 3014 x 0.4) γ
Hence, γ = 20.5 dyne cm-1
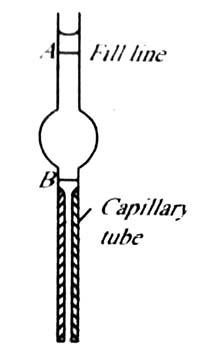
Another way of using the drop formation on the tip of a capillary for surface tension measurement is the drop volume method. A drop pipette (Figure 2) is filled with one liquid whose surface tension is known. The liquid is allowed to drop slowly and the number of drops counted until the lower meniscus travels from A to B. The experiment is repeated with the test liquid and again the number of drops when the meniscus travels from A to B is counted. For the two liquids the surface tension equation (1) may be written as;
m1g = 2πr γ1
m2g = 2πr γ2
so, γ1/ γ2 = m1/m2
Now the volume (mL) of one drop of liquid 1= V/n1
And the mass of one drop of liquid 1 = m1 = (V/n1)d1
Similarly for liquid 2 the mass of one drop = m2 = (V/n2)d2
where, V is the volume of liquid dropped in each case and n2 and n1 are the number of drops of the two liquids of densities d2 and d1 respectively.
Substitution in equation (1) gives;
γ1/ γ2 = m1/m2 = (V/n1)d1 / (V/n2)d2
= n2d1/n1d2