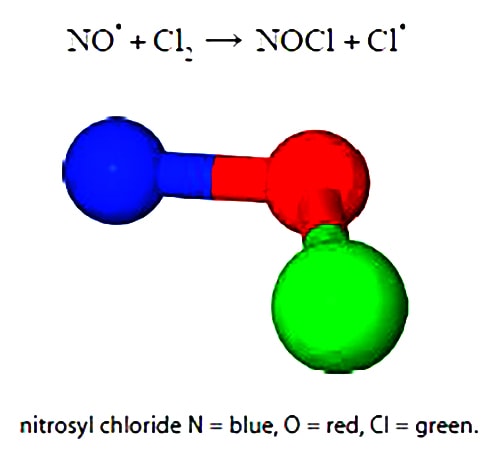
An example of a second-order reaction is the atmospheric reaction between nitric oxide (NO) and chlorine (Cl2). The superscript dots indicate radicals i.e. unpaired electrons. Nitrosyl chloride NOCl is a yellow gas first described in 1831.
The kinetics speed of a second-order chemical reaction
A + B → product
depends on the concentrations of both the molecules A and B. The rate of reaction is summarized by an equation which includes the following term as part of the equation. Where a0 and b0 are the initial concentrations of molecules A and B and x is the change in concentration of both the reactants. Simplify this expression using partial fractions.
1 / ((a0 – x) (b0 – x))
Solution
In order to simplify the expression using partial fractions we use two undefined coefficients, A and B, whose values we shall determine later on. In the partial fraction, note that the sign ≡ means “identical to” and that an identity is true for all values of x. For an equation, however, the left hand side is only equal to the right hand side for certain values of x which are called the solutions or roots of the equation.
1 / ((a0 – x) (b0 – x)) ≡ A/(a0 – x) + B/(b0 – x)
Multiply left and right of the identity by (a0 – x) (b0 – x) and cancel out where possible in any single term.
((a0 – x) (b0 – x)) / ((a0 – x) (b0 – x)) ≡ (A(a0 – x) (b0 – x)) / (a0 – x) + (B(a0 – x) (b0 – x)) / (b0 – x)
1 ≡ A (b0 – x) + B (a0 – x)
This identity is true for all values of x. Firstly, to find the unknown constant B we set x = h0.
1 ≡ A (b0 – x) + B (a0 – x); 1 ≡ (A*0) + B(a0-b0); B ≡ 1/(a0 – b0)
Secondly, to find the unknown constant A we set x = a0.
1 ≡ A (b0 – x) + B (a0 – x); 1 ≡ A(a0-b0) + (B*0); A ≡ 1/(b0 – a0)
1 / ((a0 – x) (b0 – x)) ≡ A / (a0 – x) + B / (b0 – x) ≡ 1 / ((b0 – a0) (a0 – x)) – 1 / ((b0 – a0) (b0 – x))
Notice the minus sign, we can introduce brackets to dean things up on the right hand side.
Note that, A = – B, or,
A ≡ 1/(b0-a0); B ≡ – 1/(b0-a0)
Substituting these later values for A and B into our original identity for partial fractions (in yellow) gives,
1 / ((a0 – x) (b0 – x)) ≡ 1/(b0-a0) * ((1/(a0 – x) – 1/(b0 – x))