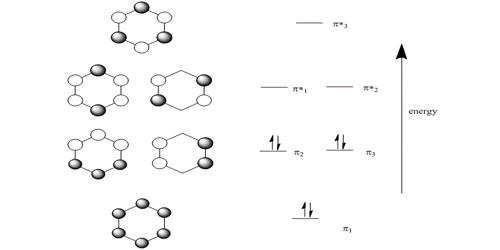
HMO theory is an approximate theory that gives a quick picture of the molecular orbital energy diagram of organic conjugated molecules.
(a) Write down the Hiickel secular determinant for the four C-atoms of cyclobutadiene in terms of x, where x = (α – E)/ β.
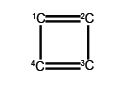
(b) Solve the secular determinant for x and then rewrite the solution in terms of (α – E)/ β and so find the allowed quantized energies (eigenvalues).
(c) Evaluate the normalized wavefunction (eigenvector) for each energy (eigenvalues).
(d) Which of the wavefunctions is the HOMO, a non-bonding NBMO or a LUMO for cyclobutadiene?
Solution
We will apply the general method for cyclic molecules to cyclobutadiene. The secular determinant is,

The determinant has an extra “1” in the (4,1) and the (1,4) corners compared to the acyclic butadiene, this is because of its “closed-up” ring structure. The general method for the energies (eigenvalues) of a cyclic conjugated hydrocarbon is slightly different from the acyclic version due to the slightly different secular determinant with the extra “1” in the (n,l) and (1,n) corners. The cyclic molecule solutions for the eigenvalues and eigenvectors are distantly related to the motion of a particle on a ring. The particle may travel clockwise or anticlockwise around the ring, thus there are two possible solutions for the eigenvectors. That is, they possess cyclic-conjugated double bonds. Each ring atom has a p orbital that is perpendicular to the ring plane.

The cosine is in radians where n = total number of carbon atoms forming the ring and k = quantum number identifying the MO where k may take the values,
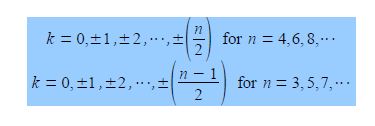
Note that for “even” rings k runs to the positive value of n/2 but for “odd” rings that k runs to plus and minus (n-1)/2. For cyclobutadiene n = 4 and so k may take the values k = 0, ±1, and +2 only i.e. there are four solutions to the quartic equation in x derived from the 4×4 secular determinant.

So there is one bonding, two degenerate non-bonding and one antibonding MOs for cyclobutadiene. There are four π-electrons, two of them are paired up in the ψ1, bonding MO, the other two are placed one each in the two degenerate non-bonding MOs with their spins parallel because of Hund’s rule of maximum multiplicity.

The π-electron energy is 2(α + 2 β) + 2α = (4α + 2β). The energy of two isolated double bonds (as in two ethene molecules) is 2(2α + 2β) = (4α + 4β). The net stabilization energy of cyclobutadiene is – 2β i.e. cyclobutadiene is destabilized by 2β compared with two isolated double bonds and thus is very reactive and will react as a di-radical. It is unstable above 35 K and dimerizes by a Diels-Alder reaction. As expected cyclobutadiene is not aromatic and it does not have aromatic stability as it does not have (4n+2) π-electrons as in Hiicicel’s rule for monocyclic compounds.
To determine the eigenvectors for a cyclic molecule we need to solve the general Hiickel matrix equation shown below for generalized cyclic molecules.
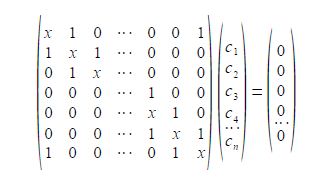
The general solution for the wavefunctions are complex (contain an imaginary part due to the motion of the particle in either direction around the ring) but the real functions may be found from linear combinations the solutions in pairs. The two real solutions are given below,

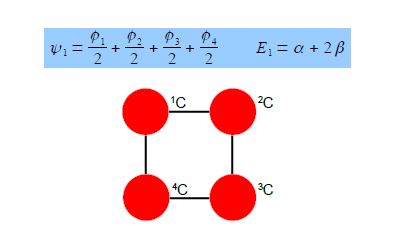
The four coefficients are all in phase and form a delocalized π-bond around all four carbon atoms. This is the lowest energy Hiickel MO conventionally labeled ψ1 and the normalization constant is N2 = 4 so N = 2.
The eigenvectors for k = +1 and k = —1 are,
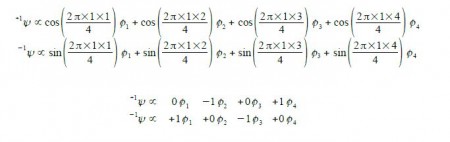
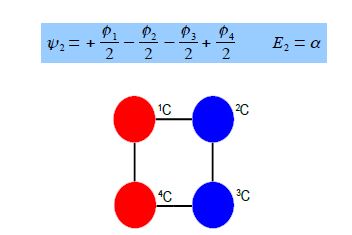
Thus for k = ±1, the two real wavefunctions correspond to the two degenerate nonbonding SOMO wavefunctions. For degenerate wavefunctions then any linear combination gives a valid wavefunction. The sum and the difference of ψ+1 and ψ-1 are ψ2 = ψ+1 + – ψ and ψ3 = ψ+1 – ψ-1. They are given below after normalization by diving by 2. These degenerate pair of wavefunctions each consists of two isolated double bonds,
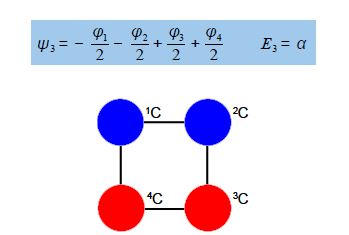
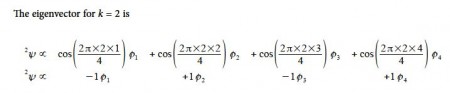
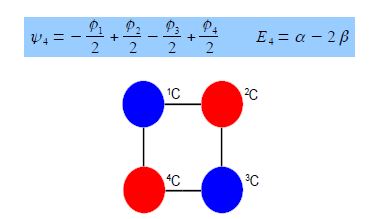
Thus for k = 2 the four coefficients are all out of phase with both of their neighbors forming a completely π-antibonding MO. This is the highest energy Hiicicel MO ψ4 and the normalization constant is again N = 2.
Although the Hiicicel method is now replaced by computer-based semi-empirical, ab initio, or DFT methods the Hiickel approximation is still great for allowing us to manually solve molecular orbitals and see what is behind these more sophisticated methods as well as giving us a good qualitative feel for the properties of the important class of both acyclic and cyclic conjugated molecules. The Hückel theory treats only π electrons in a planar conjugated molecule.