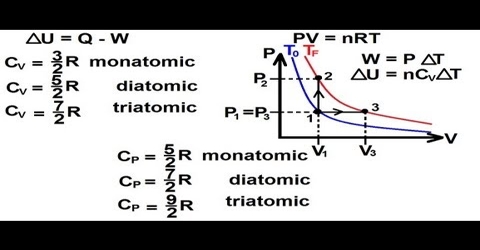
When a gas is heated at constant volume the heat supplied is used to, (a) increase the translational kinetic energy of the gas molecules and (b) to increase the intra-molecular energy, e.g., vibrational or rotational energy within the molecules.
According to the kinetic theory of gases;
PV = 2/3 x K.E.
or, K.E. = 3/2 PV
But, PV = RT for one mole of gas.
Therefore, the K.E. of one mole = 3/2 RT
For an increase of temperature from T1 to T2 the increase of Kinetic Energy of one mole of gas is,
3/2 R (T2 – T1)
When the increase of temperature is 1°C, i.e., (T2 – T1) = 10 C, the increase in K.E. is equal 3/2 R. But the molar heat capacity CV = Increase of K. E. for increase of temperature by 1°C + increase in infra-molecular energy.
Hence,
CV = 3/2 R + x … … … (1)
where x = contribution to the molar heat capacity for increase of intra-molecular energy. If the gas is monatomic there is no rotational or vibrational motion and x = 0. So, for monatomic gases:
CV = 3/2 R
When the gas is heated at constant pressure the gas expands and does work against the external pressure. Heat is required for this work to be done and also to raise the temperature. This work is equal to (PV2 – PV1) or P (V2 – V1) where V2 and V1 are the volumes at temperature T2 and T1 respectively.
When one mole of gas is considered, V2 and V1 are the molar volumes. lf T2 –T1 =1°C, then for a monatomic gas the molar heat capacity at constant pressure CP is given by;
CP = CV + P (V2 – V1)
= CV + R (T2 –T1)
= CV + R
or, CP – CV = R
In the general case where contribution from increase in intra-molecular energy is also to taken into account;
CP = CV + R + x
= 3/2 R + R + x
= 5/2 R + x