Explanation of perfect gases using kinetic theory of gases
The gases which follow fundamental postulates of kinetic theory of gases and at all temperatures and pressures simultaneously obey both Boyle’s law and Charles’s law are called ideal gases.
An ideal gas is a gas whose pressure P, volume V, and temperature T are related by the ideal gas law: PV = nRT, where n is the number of moles of the gas and R is the ideal gas constant.
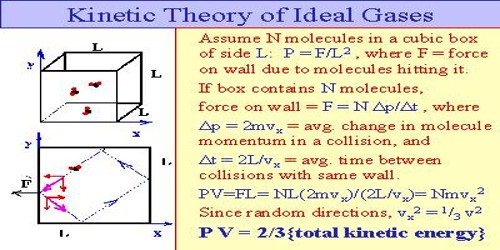
Using kinetic theory of gases ideal gas equation can be explained.
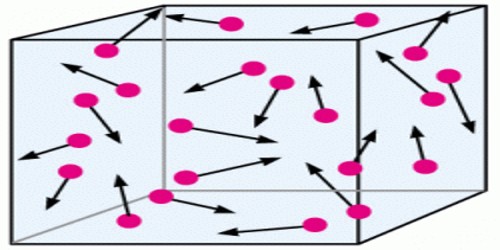
According to kinetic theory of gases heat energy of a gas is the result of kinetic energy of its molecules. In absolute zero temperature heat energy of molecules of a gas is zero. As a result kinetic energy of the molecules and root mean square velocity also becomes zero. When heat is supplied to a gas, it appears as the kinetic energy of molecules.
K.E. = ½ mnc2 = ½ Mc2
Here, m = mass of each molecule, n = number of molecules, c = root mean square velocity and M = mn = mass of the gas.
We have seen earlier that average kinetic energy of a gas is proportional to the temperature.
So, We get,
½ mnc2 ∞ T;
or, ½ Mc2 = T
Here, K = proportionality constant.
But from the equation of pressure of a gas we get,
P = 1/3 mnc2/V = 1/3 Mc2/V
or, PV = 1/3 Mc2 = 2/3 x 1/2 Mc2 = 2/3 KT
or, PV = RT
Here, R = 2/3 K = constant
then, PV = RT is called the ideal gas equation.
It is to be mentioned that V = volume of one gm at gas molecules. If n gm gas is considered, then from ideal gas equation becomes PV = nRT. It is proved from the kinetic theory of gases.