Causes of Deviations of Real gas from ideal Behavior
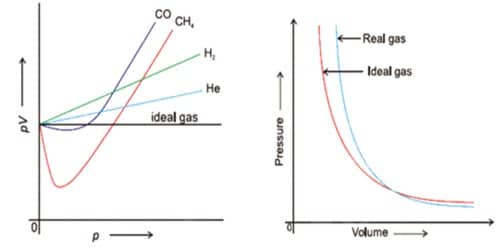
From, the Amagat’s curve we know that real gases deviate from ideal behavior. This deviation can be described by the compressibility factor which denoted by Z.
Z = PV/RT
For, 1 mole of gas PV=RT, so the value of Z for an ideal gas always 1. But for real gases the value of PV changes with the change of pressure. So the Value of Z changes. That means real gases deviate from ideal behavior. The deviation of real gases from ideal behavior becomes greater with the difference of Z from 1.0. According to Vander Waals concept, the deviation of real gases from ideal behavior depends on two factors.
- Volume Defect (error)
- Pressure Defect (error)
They are explained as follows-
- Volume Defect:
One of the postulates of the kinetic theory of gases is that the volume of a gaseous molecule is negligible compared to the volume of the container. Based on one of the postulates of the kinetic theory of the gases it is implicit that the volume occupied by the gaseous molecules themselves is negligible little compared to the total volume of the gas. But practically could be liquefied solidified at low temperature and high pressure. This postulate holds good for ideal gases and only under usual conditions of temperature and pressure for real gases. This solid or liquid have some volume which could not be neglected. When temperature is lowered significantly, the total volume of the real gas decreases enormously and becomes equivalent to the real volume of gaseous molecules.
The entire volume ‘V’ is not available for the movement of the molecules. According to Vander Waal, the volume available for the free movement of the molecules in the container will be V-b; where ‘b’ is Vander Waal’s constant. In such cases, the volume engaged by the gaseous molecules cannot be deserted in assessment with the total volume of the gas. For n mole of gas, the corrected volume will be (V-nb). Therefore, real gases omitting their own volume couldn’t obey the ideal gas equation, PV=nRT deduced from kinetic eqn.
Thus, the volume deviations created at high pressure and low temperature make the real gas to deviate from the ideal behavior.
- Pressure Defect:
According to the kinetic theory of gases we know, the gaseous molecule has no intermolecular attraction, but it is not true, because gases can be liquefied by applying pressure and decreasing temperature. For an ideal gas, the forces of magnetism between the gaseous molecule are measured to be nil at all temperature and pressure. This statement proves that it has some intermolecular attraction. For a real gas, this postulation is suitable only at low pressure or at high temperature. Under these situations, the volume of the gas is high and the molecules lie far separately from one another. Therefore the intermolecular force of attraction becomes insignificant.
So the actual pressure for a real gas will be ‘Pt intermolecular attraction force’ where P indicates pressure of an ideal gas and intermolecular attraction force is; n2a/V2
Here,
n=number of moles
a=Vander Waal’s constant
v=Volume of the container.
Therefore, real gas omitting their intermolecular attraction force couldn’t obey the ideal gas eqn, PV=nRT. The intermolecular forces of attraction become appreciable and cannot be neglected.
From the above two defects, the ideal gas eqn can be written as,
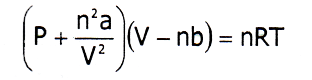
This equation is applicable for a real gas which is known as Vander Waal’s equation.