The probability P that an electron is a distance r from the nucleus is called the radial distribution function. The hydrogen atom’s is electron radial distribution function is
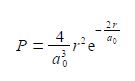
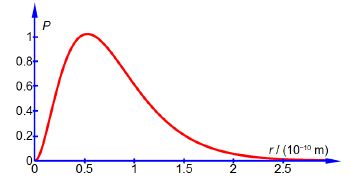
Where a0 is a constant called the Bohr radius (a0 = 0.5292 A or a0 = 0.5292 x 10-10 m). Below Figure plots the hydrogen atom’s is electron radial distribution function with a0 = 0.5292 A.
What is the probability of finding the electron at a radius of less than 2a0, i.e. integrate the above equation from r = 0 to r = 2a0
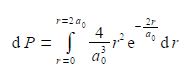
Make use of the standard integral below.
ʃ x2 ebx dx = ebx [ x2/b – 2x/b2 – 2/b3] + C
So,
The required probability comes from integrating the radial distribution function between r = 0 and r = 2a0. Firstly, take the constant term (4/a03) outside the integral.
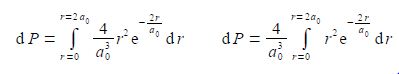
The integral is now recognizable in terms of the standard integral below.
ʃ x2 ebx dx = ebx [ x2/b – 2x/b2 – 2/b3] + C
Using the substitutions x = r and b= —2/a0 and not forgetting the constant (4/a03), the probability integral is
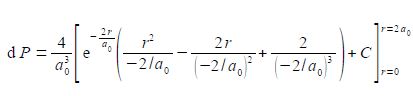
The best way to deal with this complicated looking integral is to clean-up the denominators.
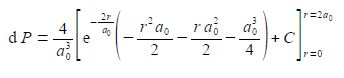
We now substitute in the two limits for our definite integral and the integration constant cancels out.
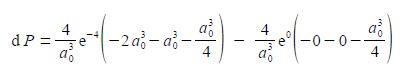
As e0 = 1, and cancelling out terms we obtain,
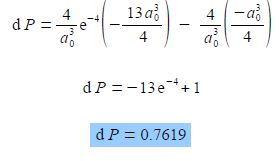
So there is 0.7619 fractional probability (i.e. fraction of unity) that the electron will be within 2a0 of the nucleus for the is atomic orbital of the hydrogen atom. This is the same as saying there is a 76.19% chance that the 1s electron is between the nucleus and a distance of 2a0. See Figure for the radial distribution function and this Figure for the 3-dimensional is atomic orbital drawn to enclose 90% of the total probability.