The rate of a chemical reaction depends upon the rate constant and the concentrations of the reagents and products each raised to a power, the powers are called the order with respect to that compound. For example, if we consider a particular chemical reaction involving H2 the rate of the reaction is
v = k [H2]x
where v is the rate of reaction, k is the rate constant (don’t get these two different terms confused) and x is the order with respect to H2. The following data for the rate of reaction is given in terms of seconds and pressure in torr (1 bar = 750 Torr to three significant figures) the pressure is proportional to concentration at a constant T.

Plot a log-log graph of the experimental data and assuming that the order x is either an integer or a half-integer for this reaction, determine x the order with respect to [H2]. Having determined the order x, find the rate constant for the chemical reaction at the temperature T of the H2 gas.
Here,
v = k [H2]x
We will (1) take logs on both sides of the equation; (2) expand out the log of a product; and (3) bring the power of the log down.
log (v) = log k [H2]x
log (v) = log (k) + log [H2]x
log (v) = log (k) + x log [H2]
This has the form of y = c + mx with the y = log(v), the intercept c = log(k) the log of the rate of reaction, the gradient m =x the order of the chemical reaction with respect to H2 and = log([H2]). Don’t confuse the order of reaction x and the general variable x (as in x, y). Note this is written deliberately in terms of using x as the power because examiners are sneaky enough to try and confuse you!
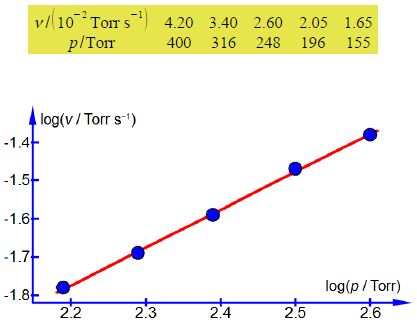
The values of the gradient and intercept from a full size manual plot are
m = 0.9992; c = —3.9741
So x = 0.9992 which as the order for this chemical reaction is expected to be an integer or half-integer, gives x = 1.0 first-order.
Having determined x, we can now find the rate constant for the reaction at this temperature
c = log (k/s-1) = -3.9741
k / s-1 = 10-3.9741
k = 1.06 x 10-4