Two chemical reactions consecutively follow on from one another. Consecutive reactions are generally very common in biochemistry and organic chemistry.
K1 k2
A → B → C
A common situation is for k1, to be a first-order rate constant at which A is transformed to B and k2 the first-order rate constant at which B transformed to product C. Assuming that we start at time zero with pure A and no B or C present then this mechanism gives the concentration of B, [B], at any later time, t, as
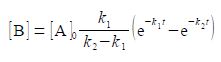
where [A]o is the initial concentration of A. Find the time, in terms of the rate constants k1 and k2, at which the concentration of B is a maximum [B]mas.
Here,
[B] = [A]0 [k1 /(k2 – k1) (e-k1t – e-k2t)
To find the maximum concentration of B we differentiate [B] with respect to t. Notice that on the right hand side the terms before the bracket are constant and differentiating with respect to t, gives
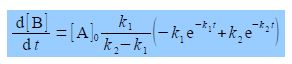
The maximum in [B] occurs when d[B]/dt = 0, which is either when [A]0 k1/(k2 — k1) is equal to zero (which it cannot be) or alternatively the term is brackets equals zero.
k1 e-k1t = k2 e-k2t
Taking natural logs allows us to find t at which [B] is a maximum.
ln (k1) – k1t = ln (k2)— k2t
ln (k1) – ln (k2) = t (k1—k2)
In (k1/k2) = t (k1—k2)
t = [1 / (k1—k2)] In (k1/k2)
The time at which the concentration of B is a maximum depends only on the values of the two rate constants and is independent of the initial concentration of A.