The kinetic gas equation can also be represented in the form of mass or density of the gas. It can be defined as the work needed to accelerate an object of a given mass from rest to its stated velocity.
Derivation of the Kinetic Equation
Kinetic energy is an uncomplicated perception with an easy equation that is easy to derive. Kinetic energy depends upon the velocity and the mass of the body. If the velocity of the body is zero then the kinetic energy will also be zero.
The pressure exerted by a gas is the total effect of the impacts of the gas molecules on the walls of the container. The expression for the pressure of a gas in terms of the molecular velocity may be derived as follows:
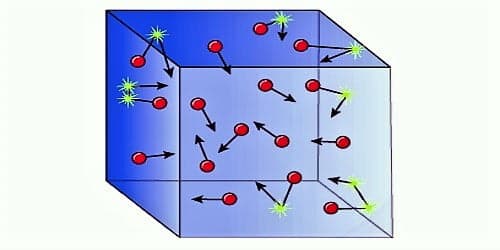
Consider a cube with sides l cm each, which contains n molecules of a gas, the mass of each molecule being m.
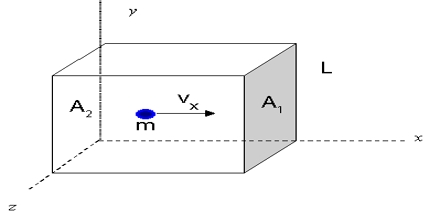
Let the root-mean-square velocity of the molecules be c. Due to the persuade of temperature, the gas molecules move in chance directions with a velocity ‘v.’ This may be resolved into three mutually perpendicular components u, v and w along the x, y and z-axes respectively, c and its components (which are vector quantities) are related by the expression
c2 = u2 + v2 + w2
The molecules are moving at random within the container and are colliding with each other and the walls of the container. Consider one molecule starting from the wall B and moving in a straight line perpendicularly to the wall A opposite to it, and rebounds:
- The momentum of the molecule before impact with the wall A = mu
- The momentum of the molecule after the impact with the wall A = -mu.
- Therefore, the change in momentum = mu-(-mu) = 2mu
This will be the momentum imparted to the wall by each impact. Before the molecule can strike the wall A again it has to travel a distance 2l to the face B and back.
- The time required to travel from A to B and back to A = 2l/u
- Hence the number of impacts on the wall A by one molecule in one second will be u/21
The total change in momentum per second for one molecule due to impacts with wall A = 2mu.u/2l = mu2/l
As the number of molecules is n the total change of momentum in one second for all the molecules = mnu2/l
The rate of change of momentum is equal to the force on the wall A. Hence force is given by:
f = mnu2/l
An experiment shows that the force exerted on the walls is the same for all the walls. Hence the velocities resolved along three axes must be equal. i.e.
u2 + v2 + w2 = c2 = 3u2
or, u2 = c2/3
therefore, force = f = mnc2/3l
Dividing both sides by l2 one obtains,
f/l2 = mnc2/3l3
But, f/l2 is force per area, which is equal to the pressure, P, and l3 is the volume, V, of the container cube,
Hence P = mnc2/3V
PV = 1/3 mnc2
This is the kinetic equation for gases. Although the above deduction has been made for a cubical vessel the equation is valid for a vessel of any shape as the vessel can be divided into a large number of small tubes for each of which this equation is valid.
We use this equation to estimate the root mean square velocity of gas molecules at any given temperature and pressure.