When substances react in a closed system, they eventually form a mixture of the constant composition of products and unreacted reactants, in a dynamic chemical equilibrium.
A dynamic chemical equilibrium consists of a forward reaction, in which substances react to give products, and a reverse reaction, in which products react to give the original reactants. Instead of the usual arrow to represent a dynamic equilibrium, we write the symbol associated with equilibrium reactions as:
Approaching equilibrium
The stable equilibrium position can be obtained by starling with:
- The reactants only
- The products only
- Or from a mixture of all of these.
Once the equilibrium has been established, the composition of the equilibrium mixture will be exactly the same, no matter which direction the equilibrium was approached.
Consider the following reaction:
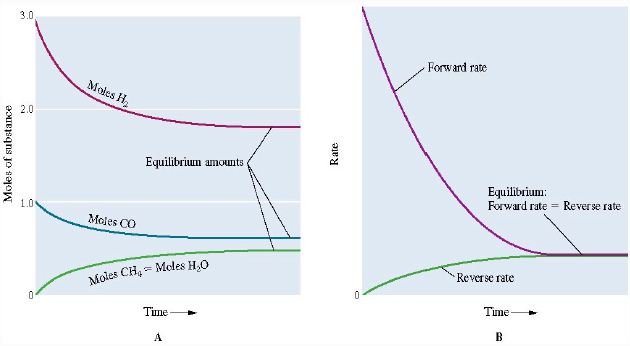
CO (g) + 3 H2 (g) ↔ CH4 (g) + H2O (g)
When CO and H2 are mixed, the concentrations of CO and H2 will rapidly decrease. Similarly, the concentration of CH4 and H2O will rise.
As both the concentrations of CH4 and H2 O increase the reverse reaction reforming CO and H2 will start to occur. Eventually, the rates of the forward and reverse reactions will become equal meaning that the reaction has reached an equilibrium as shown in the figures below.
Applying stoichiometry to an equilibrium mixture: If the starting concentrations of all the reactants are known, and the concentration of one substance at equilibrium, then the equilibrium concentrations of all the substances can be calculated.












