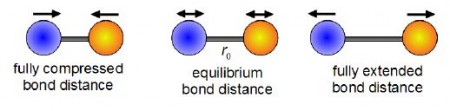
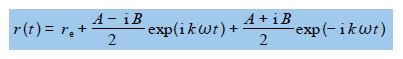Chemists use infra red spectroscopy (IR) which relies on the vibrations of chemical bonds to identify particular “functional groups” in an organic or inorganic compound and as a method of identifying unknown molecules. Below Figure shows the bond stretching and shortening in a diatomic molecule’s bond length with time from a fully compressed distance, through the equilibrium (lowest energy) distance, to the fully extended bond length and then all the way back again.
The theory behind this important spectroscopic technique makes use of a simple mathematical model to describe the vibration of a chemical bond which is called simple harmonic motion (SHM). The length of a chemical bond undergoing SHM can be described by the following equation.
E (t) = re + A cos (kɷ t) + B sin (kɷ t)
Where t is lime; ɷ is the angular frequency in radians per second of the vibration with ɷ = 2πv where v is the ordinary frequency in hertz (s-9; A and B are arbitrary constants; re is the equilibrium bond distance; and k is the force constant or “stiffness” of the chemical bond.
The periodic motion of the atoms in a vibration are more naturally modelled using complex numbers rather than trig functions as the bond length varies in a cyclic fashion with time. Write down an alternative expression for this SHM equation in term of a complex exp (i k ɷ t) and its complex conjugate.
Solution
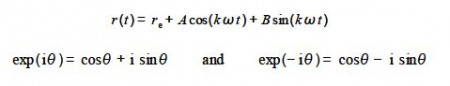
Euler’s formulae for positive and negative exponentials may be added together and after rearrangement gives cos(θ) in terms of complex numbers. Subtraction and rearrangement gives sin(θ) in terms of complex numbers. Note that we only need to remember Euler’s formulae we do not need to remember the trig equations, certainly I don’t remember them.
![]()
We can now substitute for cos (kɷ t) and sin (kɷ t) in our equation for simple harmonic motion where we have let θ = kɷ t.
![]()
In the last two terms we are diving by i which is the same as multiplying by —i which is shown below as an aside and comes from multiplying and dividing by i,
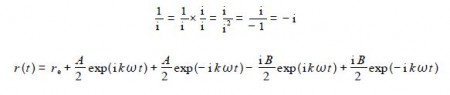
Collecting the terms with the same exponents gives: