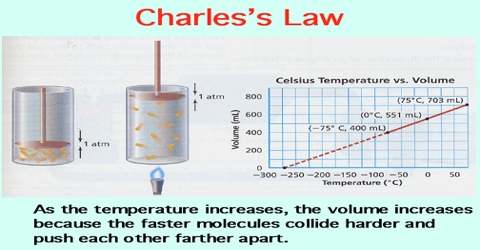
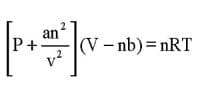Charle’s Law or Gay-Lussac’s Law
All gases increase in volume when their temperature is raised. If numerical data of the volume of a given quantity of gas held at constant pressure are plotted against temperature in the centigrade scale (as shown in Figure) it is found that the points fall on a straight line. This indicates a linear relationship between volume and temperature when the pressure is kept constant.
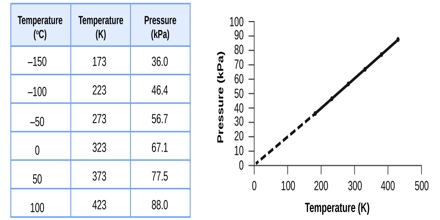
Fig: Volume of a given mass of gas vs temperature in Celsius.
If the temperature is sufficiently lowered, the gas liquefies and no more experimental points can be obtained. However, if the straight line joining the experimental points is extended as shown by the dotted line, it cuts the point of zero volume at a temperature of —273.16°C Experiments have shown that this temperature, i.e. — 273.16t does not depend on the nature of the gas provided it is stable, nor does it depend on the pressure at which the experiment is performed. This temperature is known as the absolute zero of temperature (°A) and is the lowest temperature theoretically possible. 0°C would be the same as 273.16 °A. Similarly 100°C would be (100 + 273.16 =) 373.16 °A.
Temperatures below absolute zero would correspond to negative volume, which does not have any physical meaning. In the absolute scale, the temperature is also recorded as °K (degree Kelvin) or just K in honour of Lord Kelvin who first deduced this scale of temperature from theoretical considerations. The expression for the relation between the volume of a gas and temperature is known as Charles’ law in honour of the French physicist whose experiments established it (1787). The law may now be stated as follows:
The volume of a given quantity of gas is directly proportional to the absolute temperature, the pressure remaining constant.
Mathematically it may be expressed as
V ∞ T (n and P constant)
Or, V/T = k (n and P constant) (k is a constant at constant pressure)
It follows from this expression that if a given quantity of gas at a particular pressure has volume V1 at temperature T1 and volume V2 at temperature T2 then we should have
V1T1 = V2T2.