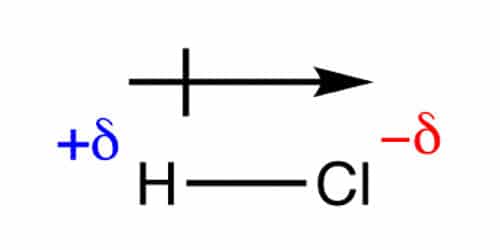
Dipole moments occur when there is a separation of charge. When atoms in a molecule share electrons unequally, they create what is called a dipole moment. They can occur between two ions in an ionic bond or between atoms in a covalent bond; dipole moments arise from differences in electronegativity. The larger the difference in electronegativity, the larger the dipole moment.
One of the most common examples is the water molecule, made up of one oxygen atom and two hydrogen atoms. The differences in electronegativity and lone electrons give oxygen a partial negative charge and each hydrogen a partial positive charge. The distance between the charge separation is also a deciding factor in the size of the dipole moment. The dipole moment is a measure of the polarity of the molecule.
As vectors have magnitude and direction, the first thing to decide is the direction of the dipole. The electric dipole moment (or just dipole moment) μ (mu) is modeled as two equal but opposite charges in a molecule Q and – Q multiplied by a distance d separating the partial charges.
μ = Q d
It is a vector that points from the negative towards the positive end of the molecule. This is the internationally agreed sign convention. Some chemists use a non-standard arrow pointing towards the negative end to signify the movement of electrons and a cross at the positive end of the molecule. It should be made dear which system is being used, we will be using the “official” convention. The SI unit of dipole moment is the coulomb meter, which is much too large for use with molecules, so dipole moments are measured in debye (symbol D) where 1 D = 3.335641×103-30 C m.
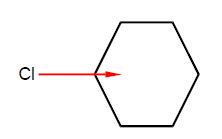
Chlorobenzene has a dipole moment of magnitude 1.5 D due to the polarized C-Cl bond. Calculate by vector addition the magnitudes and directions of the overall dipole moments for the isomers of dichlorobenzene ortho-dichlorobenzene (1,2-dichlorobenzene), meta-dichlorobenzene (1,3-dichlorobenzene), and para-dichlorobenzene (1,4-dichlorobenzene) assuming that the benzene ring is a perfect hexagon and the bond dipole μCCI remains constant at 1.5 D.
Solution
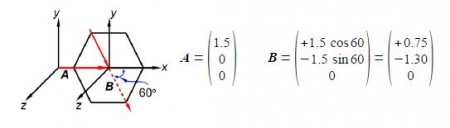
The two bond dipole moment vectors A and B each have their own components which is most clearly shown by drawing parallel Cartesian axes for the “dotted” B vector as shown below Figure. Adding the two vectors gives us the molecule’s overall dipole vector C.
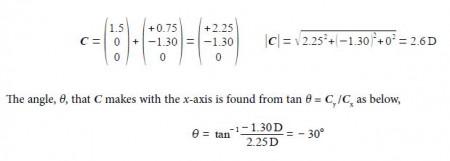
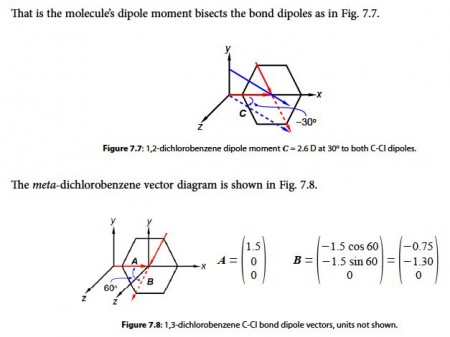
Adding the two vectors A and B gives us the molecule’s overall dipole vector C.
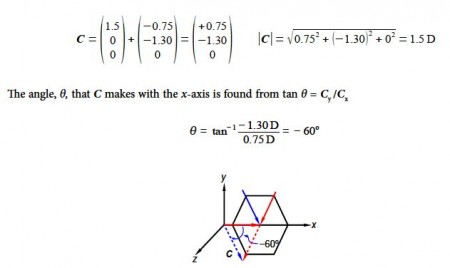
For para-dichlorobenzene the two bond dipole moment vectors are at 180° to one another and cancel out, adding the two vectors A and B gives us the molecule’s overall dipole vector C = 0 D.
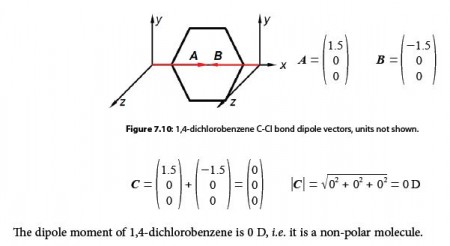
Mathematically, dipole moments are vectors; they possess both a magnitude and a direction. The dipole moment of a molecule is therefore the vector sum of the dipole moments of the individual bonds in the molecule. If the individual bond dipole moments cancel one another, there is no net dipole moment. This occurs when one atom is more electronegative than another, resulting in that atom pulling more tightly on the shared pair of electrons, or when one atom has a lone pair of electrons and the difference of electronegativity vector points in the same way.