The wavefunctions for the 2px and 2py atomic orbitals for the H-atom can be written as,
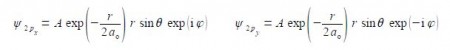
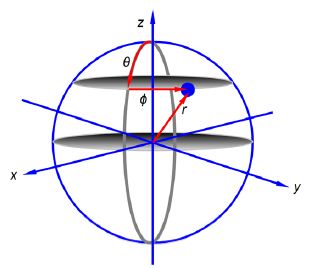
Notice that the 2px and 2py atomic orbitals only differ in the sign of the complex number term for the phi exponential. Below Figure shows the polar coordinates (r, ȹ, θ) where r is the radial distance from the origin at the centre of a sphere; θ (theta) varies from 0 at the “north pole” to it π radians at the “south pole”; and ȹ (phi) varies around the “equator” from 0 to 2π radians.
Rewrite the sum of the two wavefunctions for 2px and 2py atomic orbitals for the H-atom as a real number.
Solution
The wavefunctions for the 2px and 2py atomic orbitals for the H-atom can be written as,
![]()
To rewrite these as purely real numbers we make use of Euler’s formulae written in terms of i ȹ,
![]()
Adding our two wavefunctions,
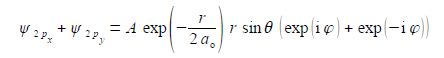
Substituting using Euler’s formulae gives the sum of the 2px and 2py atomic orbitals for the hydrogen atom which is a real function.
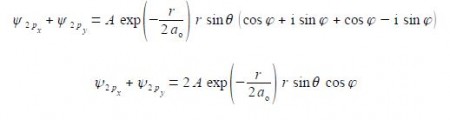
In quantum chemistry, it is often more convenient to use complex-functions, particularly when one needs to apply quantum mechanical operators to a wavefunction to generate a new wavefunction.